What is exploratory factor analysis in R?
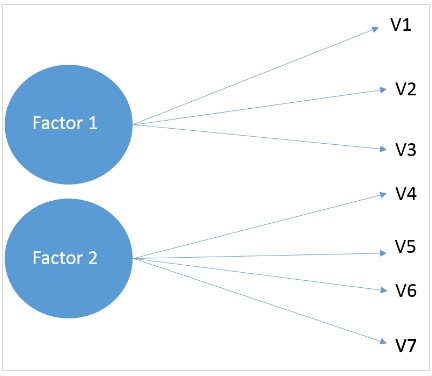
Exploratory Factor Analysis (EFA) or roughly known as factor analysis in R is a statistical technique that is used to identify the latent relational structure among a set of variables and narrow down to a smaller number of variables. This essentially means that the variance of a large number of variables can be described by a few summary variables, i.e., factors. Here is an overview of exploratory factor analysis in R.
As the name suggests, EFA is exploratory in nature – we don’t really know the latent variables, and the steps are repeated until we arrive at a lower number of factors. In this tutorial, we’ll look at EFA using R. Now, let’s first get the basic idea of the dataset.
1. The Data
This dataset contains 90 responses for 14 different variables that customers consider while purchasing a car. The survey questions were framed using a 5-point Likert scale with 1 being very low and 5 being very high. The variables were the following:
- Price
- Safety
- Exterior looks
- Space and comfort
- Technology
- After-sales service
- Resale value
- Fuel type
- Fuel efficiency
- Color
- Maintenance
- Test drive
- Product reviews
- Testimonials
Click here to download the coded dataset.
2. Importing WebData
Now we’ll read the dataset present in CSV format into R and store it as a variable.
[code language=”r”] data <- read.csv(file.choose(),header=TRUE)
[/code]
It’ll open a window to choose the CSV file and the `header` option will make sure that the first row of the file is considered as the header. Enter the following to see the first several rows of the data frame and confirm that the data has been stored correctly.
[code language=”r”] head(data)
[/code]
3. Package Installation
Now we’ll install required packages to carry out further analysis. These packages are `psych` and `GPArotation`. In the code given below, we are calling `install.packages()` for installation.
[code language=”r”] install.packages(‘psych’)
install.packages(‘GPArotation’)
[/code]
4. Number of Factors
Next, we’ll find out the number of factors that we’ll be selecting for factor analysis. This is evaluated via methods such as `Parallel Analysis` and `eigenvalue`, etc.
Parallel Analysis
We’ll be using the `Psych` package’s `fa.parallel` function to execute the parallel analysis. Here we specify the data frame and factor method (`minres` in our case). Run the following to find an acceptable number of factors and generate the `scree plot`:
[code language=”r”] parallel <- fa.parallel(data, fm = ‘minres’, fa = ‘fa’)
[/code]
The console would show the maximum number of factors we can consider. Here is how it’d look.
“Parallel analysis suggests that the number of factors = 5 and the number of components = NA“
Given below in the `scree plot` generated from the above code:
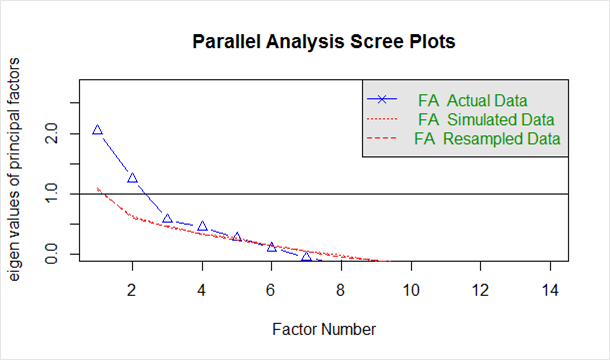
The blue line shows eigenvalues of actual data and the two red lines (placed on top of each other) show simulated and resampled data. Here we look at the large drops in the actual data and spot the point where it levels off to the right. Also, we locate the point of inflection – the point where the gap between simulated data and actual data tends to be minimum.
Looking at this plot and parallel analysis, anywhere between 2 to 5 factors would be a good choice.
Factor Analysis
Now that we’ve arrived at a probable number of factors, let’s start off with 3 as the number of factors. In order to perform factor analysis, we’ll use the `psych` packages`fa()function. Given below are the arguments we’ll supply:
- r – Raw data or correlation or covariance matrix
- nfactors – Number of factors to extract
- rotate – Although there are various types of rotations, `Varimax` and `Oblimin` are the most popular
- fm – One of the factor extraction techniques like `Minimum Residual (OLS)`, `Maximum Liklihood`, `Principal Axis` etc.
In this case, we will select oblique rotation (rotate = “oblimin”) as we believe that there is a correlation in the factors. Note that Varimax rotation is used under the assumption that the factors are completely uncorrelated. We will use `Ordinary Least Squared/Minres` factoring (fm = “minres”), as it is known to provide results similar to `Maximum Likelihood` without assuming a multivariate normal distribution and derives solutions through iterative eigendecomposition like a principal axis.
Run the following to start the analysis.
[code language=”r”] threefactor <- fa(data,nfactors = 3,rotate = “oblimin”,fm=”minres”)
print(threefactor)
[/code]
Here is the output showing factors and loadings:
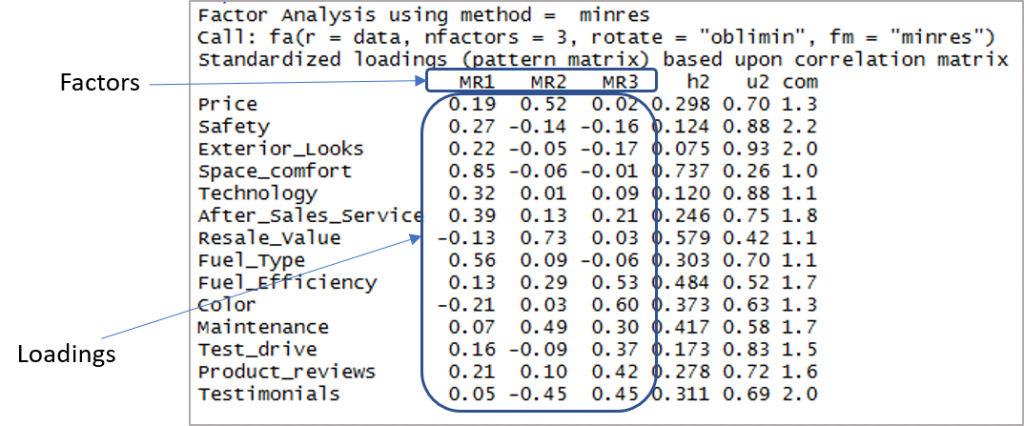
Now we need to consider the loadings more than 0.3 and not loading on more than one factor. Note that negative values are acceptable here. So let’s first establish the cut off to improve visibility.
[code language=”r”] print(threefactor$loadings,cutoff = 0.3)
[/code]
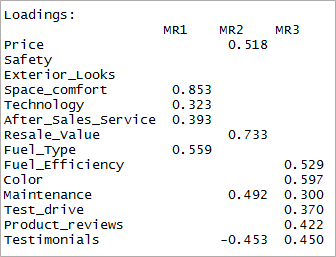
As you can see two variables have become insignificant and two others have double-loading. Next, we’ll consider the ‘4’ factors.
[code language=”r”] fourfactor <- fa(data,nfactors = 4,rotate = “oblimin”,fm=”minres”)
print(fourfactor$loadings,cutoff = 0.3)
[/code]
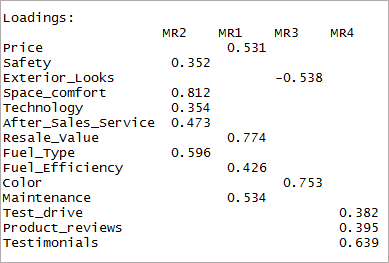
We can see that it results in only single-loading. This is known as the simple structure.
Hit the following to look at the factor mapping.
[code language=”r”] fa.diagram(fourfactor)
[/code]
Adequacy Test
Now that we’ve achieved a simple structure it’s time for us to validate our model. Let’s look at the factor analysis output to proceed.
The root means the square of residuals (RMSR) is 0.05. This is acceptable as this value should be closer to 0. Next, we should check the RMSEA (root mean square error of approximation) index. Its value, 0.001 shows the good model fit as it is below 0.05. Finally, the Tucker-Lewis Index (TLI) is 0.93 – an acceptable value considering it’s over 0.9.
Naming the Factors
After establishing the adequacy of the factors, it’s time for us to name the factors. This is the theoretical side of the analysis where we form the factors depending on the variable loadings. In this case, here is how the factors can be created.
Conclusion
In this tutorial for analysis in r, we discussed the basic idea of EFA (exploratory factor analysis in R), covered parallel analysis, and scree plot interpretation. Then we moved to factor analysis in R to achieve a simple structure and validate the same to ensure the model’s adequacy. Finally arrived at the names of factors from the variables. Now go ahead, try it out, and post your findings in the comment section.
April 4, 2017
Best tutorial on factor analysis in R on the internet…. what a weird place to find it.
April 4, 2017
Glad that you found it useful. But, why did you think that this is a weird place for such tutorial?
June 24, 2017
After so many attempts to find explanation of FA in R that actually makes sense. Thankyou!!!
July 8, 2017
Thank you. Nice tutorial
June 2, 2019
Brilliant example. Thank you.
December 30, 2017
Great tutorial! Thanks a lot.
January 2, 2018
This is the best tutorial on web…..plz upload more.
January 9, 2018
Just Awesome!
January 12, 2018
Useful tutorial, simply explained so that newbie can understand easily.
Thank you!
January 16, 2018
great, clear explanation…thanks!
January 16, 2018
A newbie has understood this complicated concept, Thanks …
February 7, 2018
This was really helpful! Now I’m ready to do a confirmatory factor analysis. I’m unable to find the post on the blog. Have you written a CFA post?
February 7, 2018
We have not yet planned for this, but I’ll try to fit this in our content calendar soon.
February 7, 2018
Thanks a lot for the great post. Did you use any special command to get RMSEA and TLI?
February 7, 2018
You’re welcome 🙂 Special commands are not required for these values.
March 2, 2018
Thank you very much, it was excellent.
March 27, 2018
Great tutorial! Very useful! Thanks!
April 13, 2018
I used the data and instructions verbatim, alas, got much different results. My loadings are different after doing the first fa() call (with the same parameters). When I do the cut-off at 0.3 in the first iteration, only Exterior_looks drops out; Safety remains in with a loading of 0.311 on MR2. Otherwise I found the tutorial very instructive; I just wish I would get verbatim results with the same input data / same set of commands.
May 11, 2018
Brilliant. This helped me a lot.
May 25, 2018
thank you. very useful. understandable. but how can ı take factor analyzing output. (which code?)
May 25, 2018
I’m not sure what exactly you mean; code is available in this tutorial.
July 15, 2018
Hi, Why the cut-off values are considered 0.3, Is there any specific reason? How do we know what cut-off should be considered? Could you please help me in understanding it.
July 20, 2018
There are no hard and fast rules. Most of the research papers suggest 0.4 or 0.3. Also, please note that with significantly high number of sample size, you can take the cut-off value at 0.2 as well.
December 4, 2018
Thanks for your help, I understood a lot.
April 1, 2019
Great tutorial, worked right away! 🙂
April 25, 2019
Thank you very much, very clearly explained
July 6, 2019
This was great!!!
Thank you very much for this great post, it’s one of the best available online!
September 9, 2019
this awesome,
please I need more information on something. if you one have identify the factors, how can you now know which variables from original data set are responsible for those factors.
September 30, 2019
Very simple and useful explanation, great work 🙂 thank you so much
October 28, 2019
Thanks a lot, very helpfull. Tried it with my data and cannot come up with a number of factros allowing single-loading only. The best possibility (with 6 factros) shiws 1 double loading, RMSR=0,05, RMSEA=0,08 (CI: 0,077-0,082) and TLI=0,597
How should I proceed if I want to imprive it ? Thanks in advance ……
November 2, 2019
you’re the best !!!
December 26, 2019
Thank you for getting back to me. That sounds great! It is a fantastic article that helps me, much indeed Information. This was really helpful!
March 2, 2020
Great explanations.
Great job…!!!!
Thank you.
March 19, 2020
Awesome! Thanks a lot
June 16, 2020
Kratom near me